구조해석에서 사용되는 '유한요소해석'의 기본 개념에 대해 알아봅니다.
유한요소해석(Finite Element Analysis, FEA)은 공학 분석에 사용되는 컴퓨터 시뮬레이션 과정을 말하며, 유한요소법(Finite Element Method, FEM)라고 불리는 수치적 기법(Numerical method)을 사용하며 구조해석 문제를 푸는 것이다.
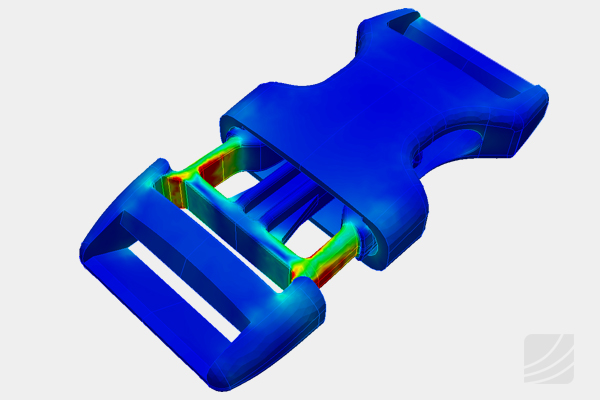
요소망, 메쉬(Mesh)는 요소(Element)와 절점(Node)으로 구성되어 있으며, 이웃한 요소들과는 노드에서 서로 연결되어 하나의 구조물을 이룬다.
외력과 경계조건에 대하여 구조물의 방정식 집합을 만들어 컴퓨터를 이용하여 해를 구하는 것이다.

수치적으로 답을 구하기 쉬운 단위인 요소(레고 블록)로 절점 공유를(서로 조립을) 하면 구조물(타노스)를 만들어 문제를 풀 수 있다.
실제 우리가 풀려고 하는 공학 문제들은 이제 반대로 접근한다.
해석하고자 하는 대상물의 도면(CAD)을 '적당한' 크기의 요소로 잘라서 메쉬를 만들고 컴퓨터로 계산하여 해를 얻는다. 이 전반적인 FEA 과정에서 ANSYS와 같은 상용 해석 패키지 프로그램을 이용한다.
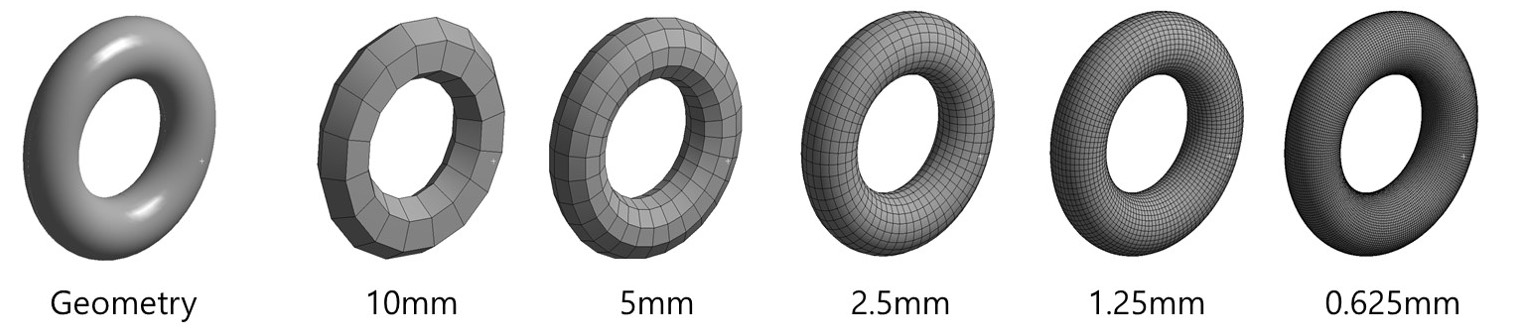
결국 메쉬를 잘게 나누면 나눌수록 근사해의 오차는 작아지며 해석의 정확도가 올라간다. 예시처럼 오른쪽으로 갈 수록 본래 형상(Geometry)을 거의 따라가는 것을 볼 수 있다.
그러나, 늘어난 요소의 숫자만큼 풀어야 할 미지수와 방정식의 숫자가 많아져(=컴퓨터의 계산량이 많아져) 해석 비용이 증가한다.
요소 크기↓ 정확도↑ but 요소들의 개수↑ 해석 시간↑ 해석 비용↑
현업에서는 유한한 자원(시간, 장비)를 사용할 수 밖에 없으므로 합당한 수준의 메쉬 사이즈를 정해서 해석을 수행하게 된다.
예를 들어, 손바닥만한 크기 부품의 0.5mm 변위를 구하는 문제에서 0.0001~0.001mm에 대한 정확도를 높이기 위해 굳이 요소를 더 작게 만들지 않는다.
FEM을 이용해서 구조해석을 하려면 Meshing이라는 이산화 과정이 필요하고,
해석 대상과 가용 자원에 따라 적절한 크기의 요소 사이즈를 선정한다.
♦ Mesh 사이즈 결정
구조해석을 처음 배우는 분들이 가장 많이 묻는 질문 중 하나가 바로 "메쉬는 얼마나 잘게 쪼개야 하나요?"입니다.
일반적으로 보면 단순히 '크기를 작게 나눌수록 정확해진다'라고 생각하기 쉽습니다.
실제로도 어느 정도 맞는 말이지만, 해석은 단순히 정확도만 추구하는 게 아닙니다.
● 메쉬가 너무 조밀하면 계산시간이 폭증합니다.
● 메쉬가 너무 거칠면 결과가 신뢰할 수 없습니다.
● 같은 부품 내에서도 세밀함이 필요한 부분과 그럴 필요가 없는 부분이 구분됩니다.
따라서, 메쉬 사이즈 결정은 정확도와 효율성 사이의 균형을 잡는 과정입니다.
1) 메쉬 사이즈와 정확도의 관계
메쉬가 세밀할수록 해석 결과는 이론값에 가까워집니다.
하지만 무조건 작은 메쉬가 좋은 건 아닙니다. 왜냐하면 해석 프로그램은 결국 유한한 계산 자원(CPU, RAM, Solver 성능) 안에서 동작하기 때문입니다.
간단한 예를 들어, 1만개 요소(Element)로 해석하면 10분 만에 결과가 나올 수 있지만, 100만 개 요소로 해석하면 하루가 걸릴 수도 있습니다.
→즉, 해석의 목적이 단순위 변위 값 대략 확인인지, 아니면 응력 집중을 정밀하게 분석하는지에 따라 메쉬 크기는 달라져야 합니다.
Tip :
⊙ 처음에는 비교적 큰 메쉬로 빠르게 예비 해석(First run)을 돌려보세요.
⊙ 이후 중요한 영역만 국부적으로 메쉬를 세밀화하는 방식(Refinement)을 쓰면 효율적입니다.

2) 모든 영역을 세밀하게 만들면 안 되는 이유
초보자들이 자주 하는 실수는 "전체 모델에 동일한 세밀한 메쉬"를 적용하는 것입니다.
이 경우 계산량은 기하급수적으로 증가하고, 실제로는 필요 없는 영역에 자원을 낭비하게 됩니다.
패널 조립품의 해석을 할 때,
→응력이 집중되는 볼트 구멍 주변은 세밀한 메쉬가 필요하지만, 넓은 평판 부분은 굳이 그렇게 세밀할 필요가 없습니다.
즉, 해석에서 중요한 건 "전체를 고르게 세밀화"하는 것이 아니라, 결과에 관심이 있고 물리적으로 의미 있는 부분만 집중적으로 세밀화하는 것입니다.

Tip :
⊙ 필렛(Fillet), 나사 구멍(Screw hole), 접촉면(contact area) 같은 곳은 세밀하게
⊙ 평평하고 응력 변화가 작은 영역은 거칠게 ↔ 응력 변화가 크고, 두께 변화, 형상이 복잡한 영역은 조밀하게
⊙ Body Sizing, Face Sizing, Edge Sizing 기능 등을 활용하면 효율적인 메쉬 분배가 가능
3) 요소 형상(Element Type)의 선택
메쉬는 단순히 크기뿐 아니라 어떤 형상의 요소를 쓰느냐도 중요합니다. (사실 매우 중요함)
● 2D 요소 (삼각형 Tri, 사각형 Quad)
● 3D 요소 (사면체 Tetra, 육면체 Hex, 프리즘 등)
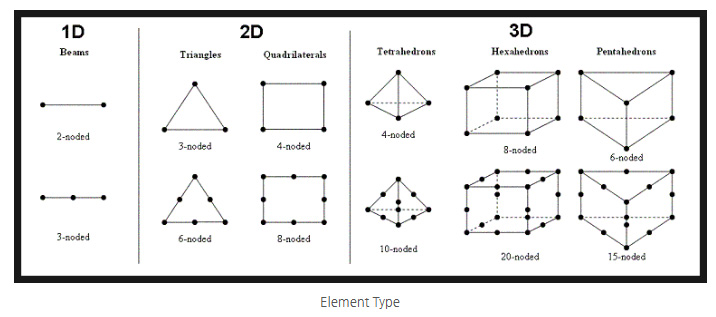
하지만 해석 정확도와 수렴성은 육면체(Hexahedral) 요소가 더 좋습니다.
따라서 단순히 "작게 쪼갠다"가 아니라, 어떤 요소를 어떻게 배치할지도 결과 정확도에 직접적인 영향을 줍니다.
Tip :
⊙ 가능하다면 단순한 영역에는 육면체(Hex) 요소 사용
⊙ 복잡한 곡면이나 구멍 주변은 사면체(Tet)를 쓰되, 필요시 국부 세밀화
⊙ 두께가 얇은 판 구조물은 계산 효율이 좋은 Shell 요소를 사용
4) 메쉬 수렴성 검증(Mesh Convergence Study)
메쉬 사이즈를 결정하는 가장 합리적인 방법은, 메쉬를 조금씩 줄여가며 결과를 비교하는 것입니다.
이를 통해 결과 값이 어느 수준 이상 변하지 않으면, 그 지점에서 메쉬를 확정할 수 있습니다.
이 방법을 Mesh Convergence Study라고 합니다.
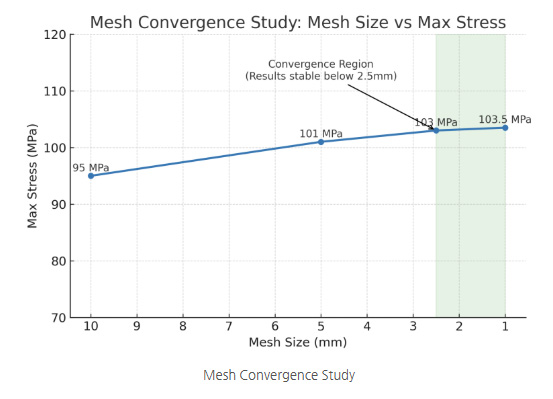
예를 들어 메쉬 사이즈 별로 결과를 비교해 보면,
● 메쉬 사이즈 10mm → 최대 응력 95 MPa
● 메쉬 사이즈 5mm → 최대 응력 101 MPa
● 메쉬 사이즈 2.5mm → 최대 응력 103 MPa
● 메쉬 사이즈 1mm → 최대 응력 103.5 MPa
→ 이 경우, 2.5mm 이하에서는 결과 값이 거의 변하지 않으므로, 굳이 1mm까지 줄일 필요가 없습니다. 요구하는 정확도에 따라 다르지만 결과의 변화가 1~2% 이내이면 중단합니다.
Tip :
⊙ 단순히 결과 한 개(예:최대 응력)만 비교하지 말고, 응력 분포 패턴도 같이 확인하세요.
⊙ 메쉬 수렴성 검증은 시간이 조금 걸리더라도, 결과의 신뢰성을 확보하는 가장 확실한 방법입니다. (한 번만 제대로 해놓으면 편해요)
※ 참고하면 좋은 영상
https://youtu.be/xytxzptxwgI
5) 초보자가 기억해야 할 균형 감각
초보자일수록 "작게=무조건 좋다"라는 착각에 빠집니다.
하지만 실무에서는 해석 정확도와 계산 효율의 균형이 최우선입니다.
예를 들어, 단순히 설계 초기 단계에서 '대략적인 변위 수준'을 알고 싶을 때는 굳이 정밀한 메쉬가 필요하지 않습니다.
반대로 피로 수명 분석이나 용접부 응력 해석처럼 국부 현상이 중요한 경우에는 정밀 메쉬가 필수입니다.
즉, 모든 해석에 하나의 정답 메쉬는 없다는 사실을 명심해야 합니다.
해석 목적, 모델 복잡도, 사용 가능한 컴퓨터 자원에 따라 최적의 메쉬 전략이 달라집니다.
메쉬 사이즈 결정은 단순히 "얼마나 잘게 쪼갤까?"의 문제가 아니라,
해석 목적에 맞춰 어디에 자원을 집중할지 선택하는 과정입니다.
정리한 원칙을 기억하세요:
"전체를 무조건 세밀화하지 말고, 중요한 영역에 집중할것"
"요소 형상과 메쉬 품질도 결과에 큰 영향을 준다는 점"
"반드시 메쉬 수렴성 검증으로 결과 신뢰성을 확보할 것"
이렇게 하면, 초보자도 처음부터 불필요한 시행착오를 줄이고 효율적인 해석을 할 수 있습니다.